"Captain', c'est bien sympa le cheval, mais tu m'expliques le lien entre les courses hippiques et l'économie ?". Et bien aussi étrange que cela puisse paraitre, il existe une littérature abondante sur cette thématique ! Depuis un article de Griffith paru en 1949 paru dans The American Journal of Psychology (source : "Odds Adjustments by American Horse-Race Bettors"), de nombreuses recherches ont été réalisées afin de tenter d'expliquer une anomalie empirique sur le marché des courses hippiques : le "favorite-longshot bias". Le quoi ? Pour faire simple, supposons qu'un cheval ait 1 chance sur 100 de gagner (outsider), et qu'un autre cheval ait 1 chance sur 2 de gagner. En moyenne donc, sur 100 courses, le favori gagnera 50 fois, et l'outsider gagnera 1 fois. En théorie donc, la côte du favori devrait être proche de 2 contre 1 (vous gagnez deux fois votre mise si le cheval gagne, un peu moins en enlevant la marge du bookmaker) et celle de l'outsider proche 100 contre 1, de telle sorte à ce que l'espérance de gain soit la même... Mais ça, c'est en théorie !
 En effet, les études empiriques ont montré qu'en moyenne, un pari sur un cheval ayant une côte de 100 contre 1 ou plus entrainait une perte de 64%, un pari aléatoire une perte de 23% et un pari sur le favori une perte de 5,5% (source : "Explaining the favorite-long shot bias: Is it risk-love or misperceptions?"). Par exemple si vous avez 1000 euros dans votre portefeuille et que vous pariez sur 1000 courses différentes 1 euro sur l'outsider de la course, vous n'aurez donc à la fin plus que 360 euros en poche, tandis que si vous pariez 1000 fois 1 euro sur le favori, il vous restera 945 euros à la fin (au global le seul gagnant est le bookmaker, bien évidemment). La différence d'espérance de gain est énorme, avec une relation inverse avec la théorie de l'aversion au risque (une des bases de la théorie financière): ici, plus un pari est risqué, moins son espérance de gain est élevé. Et c'est là que le prince économiste arrive sur son grand cheval blanc afin d'essayer de comprendre les raisons de cette anomalie (sauver une princesse c'est "has been", un économiste préfère sauver son ordinateur et faire de l'économétrie).
En effet, les études empiriques ont montré qu'en moyenne, un pari sur un cheval ayant une côte de 100 contre 1 ou plus entrainait une perte de 64%, un pari aléatoire une perte de 23% et un pari sur le favori une perte de 5,5% (source : "Explaining the favorite-long shot bias: Is it risk-love or misperceptions?"). Par exemple si vous avez 1000 euros dans votre portefeuille et que vous pariez sur 1000 courses différentes 1 euro sur l'outsider de la course, vous n'aurez donc à la fin plus que 360 euros en poche, tandis que si vous pariez 1000 fois 1 euro sur le favori, il vous restera 945 euros à la fin (au global le seul gagnant est le bookmaker, bien évidemment). La différence d'espérance de gain est énorme, avec une relation inverse avec la théorie de l'aversion au risque (une des bases de la théorie financière): ici, plus un pari est risqué, moins son espérance de gain est élevé. Et c'est là que le prince économiste arrive sur son grand cheval blanc afin d'essayer de comprendre les raisons de cette anomalie (sauver une princesse c'est "has been", un économiste préfère sauver son ordinateur et faire de l'économétrie).
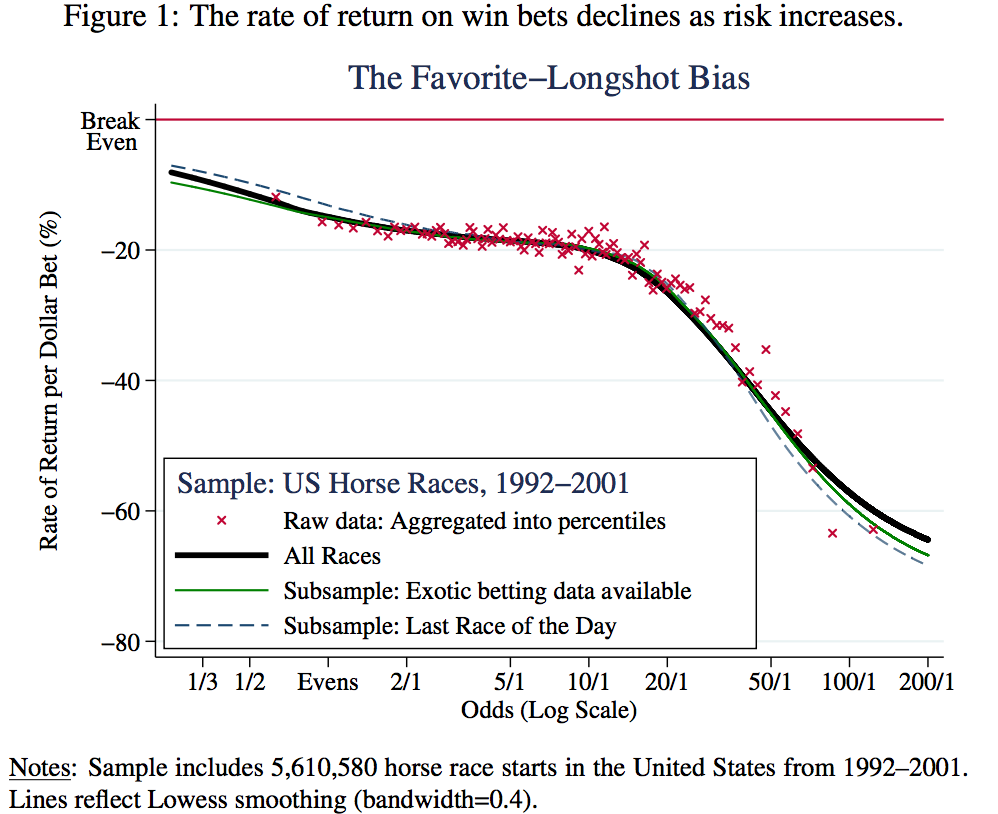
Il existe différentes théories pouvant expliquer cette anomalie : soit (1) les individus sont excités par le gain important potentiel en cas de victoire de l'outsider et sont donc prêts à accepter une espérance de gain inférieure, soit (2) les individus ont une mauvaise perception des probabilités et ne comprennent pas grand chose à tout cela. Dans le premier cas, les individus sont rationnels et cette anomalie est en réalité cohérente avec une maximisation de l'utilité/bien-être : si vous accordez une valeur supérieure au fait de perdre de l'argent en ayant parié sur un outsider, ou bien si vous valorisez l'adrénaline ou bien le fait de pouvoir vous la raconter auprès de vos collègues, et bien dans ce cas pas de problème. Si par contre il s'agit d'une mauvaise compréhension des probabilités, c'est plus embêtant pour vous (car vous perdez de l'argent sans surplus de bonheur) et c'est embêtant pour un économiste classique car il suppose que les individus sont rationnels et comprennent bien les probabilités, et là vous venez foutre le bordel dans ses modèles.
Bien qu'il soit assez difficile de séparer les deux hypothèses pour voir si l'une est dominante, l'étude de Snowberg & Wolfer présentée ci-dessous tend à favoriser la seconde hypothèse, en s'appuyant sur une méthodologie originale sur un échantillon de plusieurs millions de courses hippiques entre 1992 et 2001 :
"Our results are more consistent with the favorite-longshot bias being driven by misperceptions rather than risk-love. Indeed, while each class is individually quite useful for pricing compound lotteries, the misperceptions class strongly dominates the risk-love class"
Cette anomalie présente sur le marché des courses hippiques se retrouve aussi sur le marché des "tombolas". Si par exemple une tombola propose un gros lot de 9000 euros et un second lot de 1000 euros, et qu'il y a 10.000 joueurs, alors l'espérance de gain est de 1 euro. Les individus vont cepedant avoir tendance à préférer ce genre de tombola à une tombola proposant la même espérance de gain, mais avec par exemple 5.000 lots de 2 euros. Cela signifie qu'ils sont prêts à payer plus cher pour participer à la première tombola, pourtant plus risquée (car davantage de volatilité et de dispersion du rendement - source: "Why People Choose Negative Expected Return Assets - An Empirical Examination of a Utility Theoretic Explanation", Bhattacharyya & Garrett)
Sur les marchés financiers, cette conclusion est confirmée dans l'étude très récente "Do Investors Overpay for Stocks with Lottery-like Payoffs ? An Examination of the Returns of OTC Stocks" (Journal of Financial Economics, Eraker & Ready, 2014), dans laquelle les auteurs montrent que les actions des entreprises ayant un "lottery-like payoffs", c'est à dire dont le cours peut par exemple doubler rapidement (par exemple petite entreprise de biotechnologie avec donc une distribution des rendements avec skewness positive), ont en moyenne un rendement négatif. Idem ici, la grande question est de savoir si cette anomalie est rationnelle ou bien due à une incompréhension des probabilités. Dans le premier cas pas besoin de régulation tandis que dans le second, cela peut être utile pour "protéger" les investisseurs non-informés.
"This extra utility from the "game" could explain why investors could be willing to accept the negative expected returns for native stocks, and at the same time require normal expected returns to hold delisted stocks. If this explanation is correct, then perhaps additional regulation is unnecessary; new firms get funding for new projects and the investors enjoy the experience enough to offset the negative expected returns" - Eraker and Ready
Conclusion : Il existe tout de même une différence importante entre les marchés financiers et les courses hippiques : en moyenne sur le long-terme, le rendement est positif sur les marchés financiers, tandis que le rendement est négatif sur les paris sportifs (marge de bookmakers / casino). Pourquoi ? Tout simplement car la valeur d'une entreprise augmente en moyenne avec le temps, tandis qu'il n'y a pas de création de valeur lors d'un pari sportif (c'est un transfert d'argent entre un perdant et un gagnant). Il est donc possible que les individus soient "risk-lover" en ce qui concerne les paris (l'espérance étant négative, autant prendre du risque à fond) et "risk-averse" en ce qui concerne les marchés financiers. Et bien voilà un bon sujet de mémoire !
 Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.
Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.