Avant le week-end, le Captain' vous propose un petit jeu ! Supposons que le taux d'intérêt à très long-terme prévalant sur le marché soit de 4%. Cela signifie simplement que n'importe quel investisseur peut placer son argent à ce taux là. Il n'existe aucun risque de défaut (pas d'arnaque à la grecque de la part du Captain'). Le Captain' vous propose donc, en échange de 80 euros aujourd'hui, de vous verser 3 euros par an pendant 100 ans. Allez comme je suis sympa, je vous promets même de vous verser 3 euros par an jusqu'à la fin des temps. La bonne affaire ?
Pour répondre à cette question, il est nécessaire de déterminer la valeur actualisée de cette rente perpétuelle. La valeur actuelle correspond à la somme des flux de trésorerie générés par un titre financier ou un actif (ici 3 euros par an jusqu'à la fin des temps), actualisés au taux de rentabilité exigé (ici 4%, le taux du marché à très long-terme). Il est important de bien comprendre que recevoir 10 euros dans 1 an est moins bon que de recevoir 10 euros aujourd'hui. En effet, si vous recevez 10 euros aujourd'hui, vous allez pouvoir placer cet argent durant 1 an et à la fin de cette période vous aurez donc 10,04 euros sur votre compte en banque.
Si l'on prend le problème dans l'autre sens, quelle est la valeur actualisée d'un flux de 3 euros dans un an, si le taux du marché est à 4%. Le calcul est tout simple ; recevoir 3 euros dans un an est la même chose que d'avoir 3 / (1,04) = 2,88 euros aujourd'hui. En effet, en plaçant 2,88 euros aujourd'hui au taux de 4%, vous aurez à la fin de l'année 3 euros. Et donc quelle est la valeur actualisée d'un flux de 3 euros dans 2 ans ? Idem, sauf qu'ici il faut prendre en compte le fait que vous "perdiez" deux années de capitalisation, ce qui donne une valeur actualisée de 3 / (1,04^2) = 2,77 euros. En effet si vous placez 2,77 sur deux ans, vous toucherez la première année 0,11 euro d'intérêt que vous pourrez alors replacez, et l'année suivante 0,12 euro.
Si l'on entend le raisonnement à 100 périodes, voici la valeur actualisée de chaque flux selon l'année. Comme vous pouvez le voir, la différence entre recevoir 3 euros dans 1 an ou 3 euros aujourd'hui est assez faible ; par contre, recevoir 3 euros dans 50 ans est l'équivalent de recevoir 0,42 euro aujourd'hui et de placer cet argent à 4% pendant 50 ans.
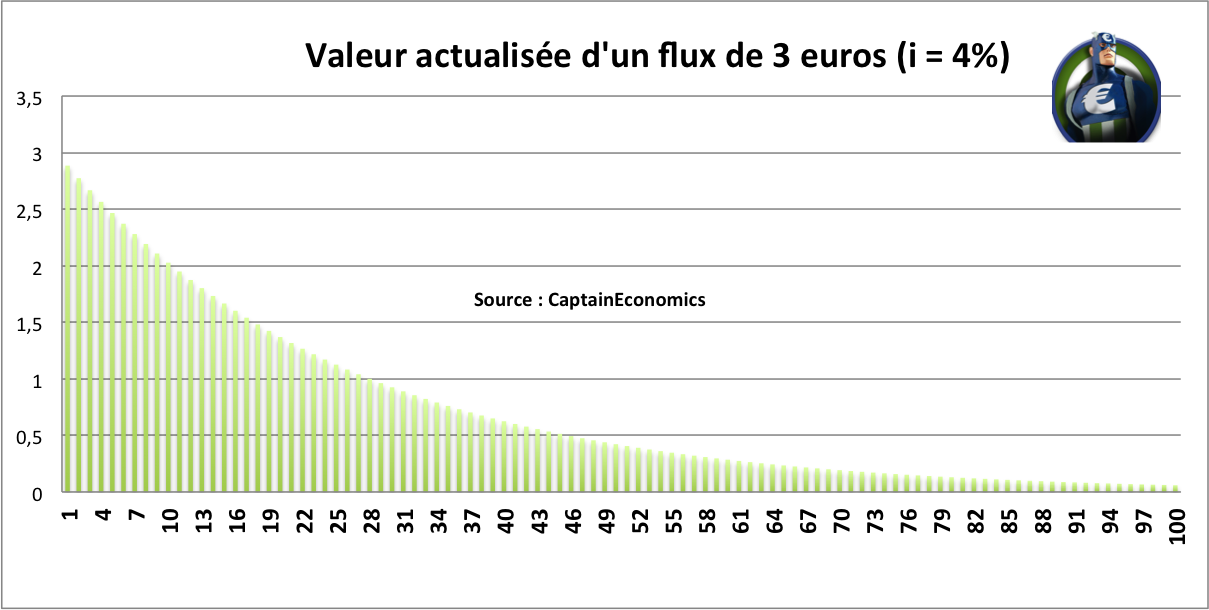
Mais alors, avez-vous intérêt à accepter le deal proposé par le Captain' ? Pour le savoir, il suffit de faire la somme actualisée des flux, afin de calculer la valeur actualisée nette totale de la proposition du Captain'.
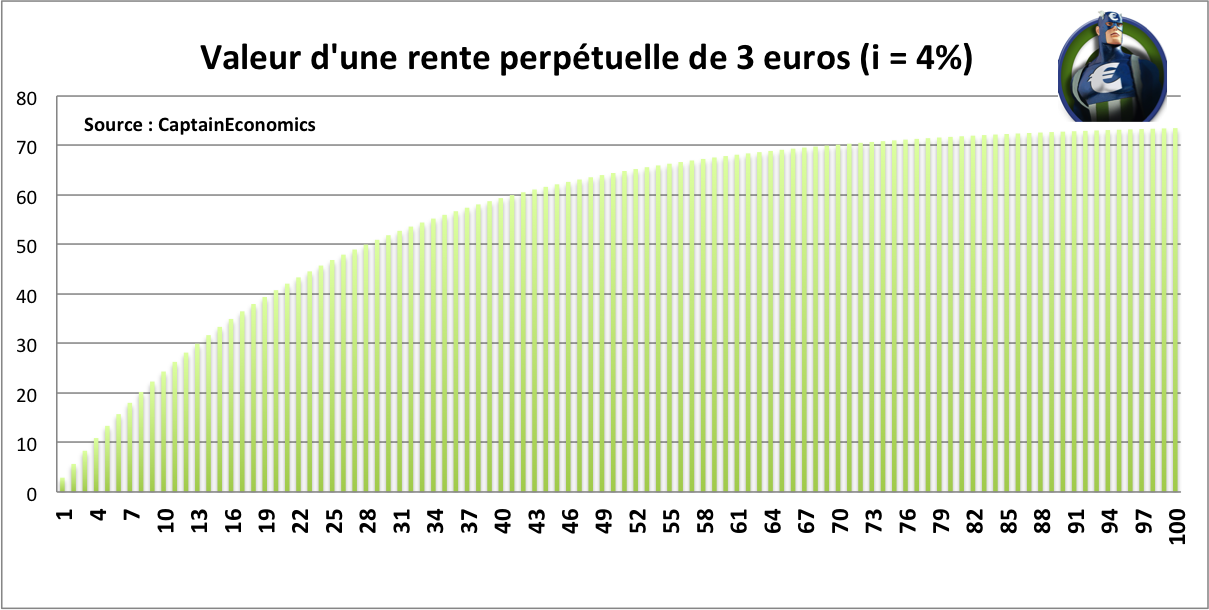
Lorsque le taux à très long terme est de 4%, la valeur actuelle d'une rente de 3 euros à vie est de 75 euros. Le calcul de la valeur présente d'une rente perpétuelle est très simple : Valeur présente = Montant du flux annuel / Taux d'intérêt. Ici, la valeur présente est donc égale à 3 / 0,04 = 75 euros. Si vous acceptez de donner aujourd'hui 80 euros au Captain' en échange de la réception d'un paiement de 3 euros par an "ad vitam aeternam", vous vous faites clairement arnaquer.
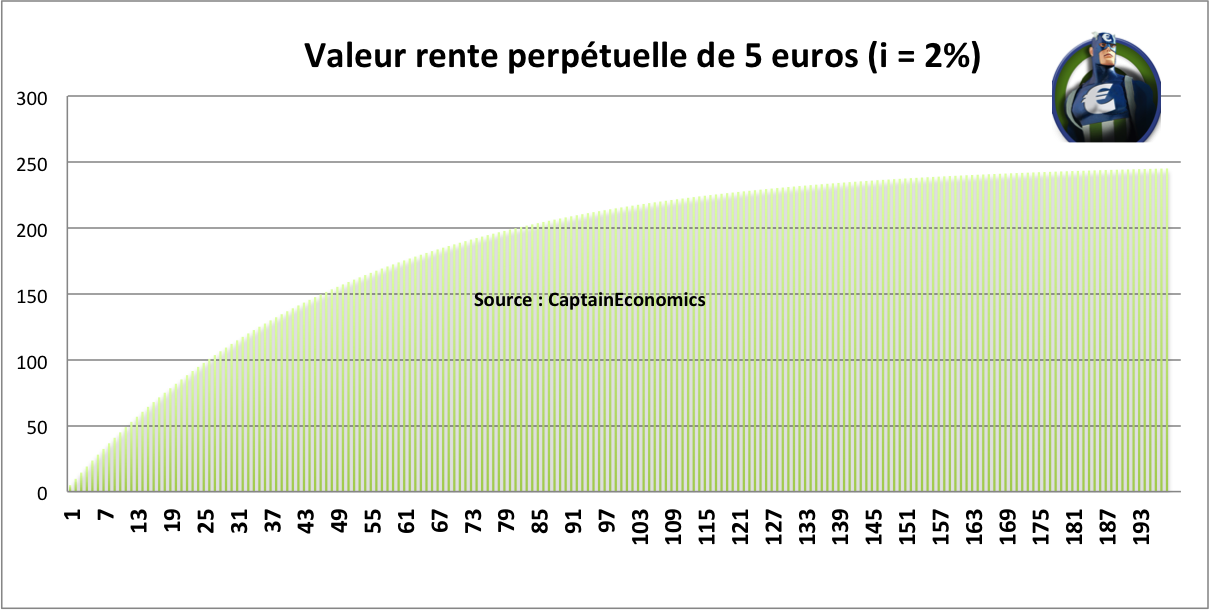
Vous avez tout compris ? Alors faisons un nouveau test. Le Captain' vous propose de vous verser 5 euros par an à vie, en échange de 200 euros aujourd'hui et en sachant que le taux à très long-terme prévalant sur le marché est de 2%. Acceptez-vous ? Pour cela, il vous suffit de calculer la valeur présente d'une rente perpétuelle de 5 euros lorsque le taux est de 2%. Valeur présente = Montant du flux annuel / Taux d'intérêt = 5 / 0,02 = 250 euros. Vous êtes donc gagnant en donnant au Captain' 200 euros aujourd'hui. Graphiquement, on voit bien que la valeur cumulée des flux tend vers 250 euros.
Conclusion : Si vous voulez vous amuser en changeant la valeur du flux annuel ou bien en modifiant le taux d'intérêt, le Captain' vous propose de télécharger la feuille de calcul ayant servi à réaliser les graphiques de cet article ici (source : "Excel Captain Valeur Actualisée"). C'est une simple feuille de calcul avec deux divisions, mais cela peut toujours être utile. Nous verrons la semaine prochaine l'impact d'une hausse ou d'une baisse du taux d'intérêt sur la valeur actualisée de la proposition du Captain' et l'influence de la durée du titre sur sa sensibilité aux taux.
Cet article est mis à disposition selon les termes de la licence Creative Commons Attribution - Pas de Modification 4.0 International. N'hésitez donc surtout pas à le voler pour le republier en ligne ou sur papier.
